 The mathematical basis for object segmentation and tracking
The mathematical basis for object segmentation and tracking
We have developed a new mathematical theory of object segmentation and invariant tracking. The property that we use to solve segmentation and invariance is surface contiguity, which is categorically different from that used in the past: it is topological not image-based. Given a stream of image frames of a scene, our strategy is not to compute whether a specific object is present within each frame through a statistical approach (the conventional solution, which delegates the core challenge of perceiving invariance to the hand picker responsible for training, i.e., the biological visual system we are trying to understand), but to decompose the image into local patches and compute for each patch the contiguous physical surface to which it belongs; the essential information for this computation turns out to reside in mappings between successive views of the environment, obtained by either having two eyes with binocular overlap, or by moving the head. This computational theory provides a new roadmap for understanding the neural basis for segmentation and tracking.
<
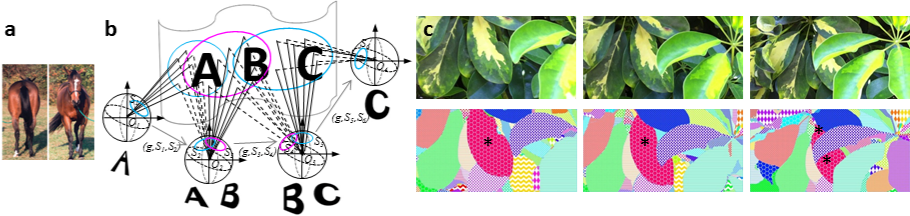
The mathematical basis for perceiving object invariance. (a) The invariance problem: how can one perceive that very different views represent the same object? (b) Mathematical formulation of the invariance problem: Image patches A and C belong to the same global object, but are never simultaneously visible. How can the visual system determine that they belong to the same object? Light rays from objects in the environment project to each observation point. One can prove that the mappings between the spheres of rays at successive observation points (four are shown) fully encode the topological structure of the environment, i.e., the global contiguous surfaces and their boundaries. (c) Top: three successive frames of leaves; bottom: a computational implementation of topological surface representation is able to successfully segment and track each leaf despite severe changes in appearance due to partial occlusion (e.g., the leaf marked by *). The biological question we want to answer is: how are these object labels computed by the brain?
A new animal model for vision
Theories of segmentation involve complex recurrent and feedback circuits. To dissect these circuits, we need methods to observe large numbers of neurons across multiple brain areas simultaneously. We are developing new tools to do this in macaques. At the same time, we would like to develop a new animal model for vision, the tree shrew. We believe the tree shrew may provide an exciting model for understanding vision, since it has 10x the visual acuity of mice, while possessing a small, smooth brain amenable to cutting edge circuit dissection tools developed for rodent-sized animals.
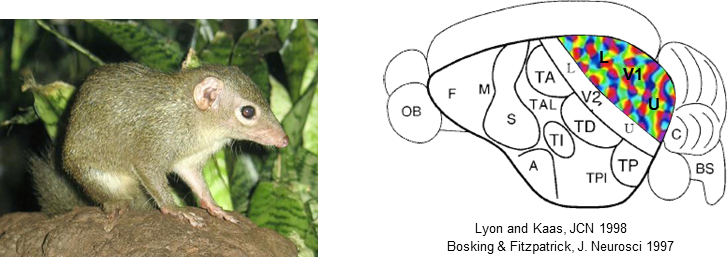 The tree shrew: a new model for vision. Left: picture of a tree shrew. Right: side view of tree shrew brain
The tree shrew: a new model for vision. Left: picture of a tree shrew. Right: side view of tree shrew brain